7.9 KiB
% Introduction to Data Analysis and Machine Learning in Physics: \ 3. Machine Learning Basics, Multivariate Analysis % Martino Borsato, Jörg Marks, Klaus Reygers % Studierendentage, 11-14 April 2023
Multi-variate analyses (MVA)
-
General Question \vspace{0.1cm}
There are 2 categories of distinguishable data, S and B, described by discrete variables. What are criteria for a separation of both samples?
- Single criteria are not sufficient to distinguish S and B
- Reduction of the variable space to probabilities for S or B \vspace{0.1cm}
-
Classification of measurements using a set of observables
(V_1,V_2,....,V_n)- find optimal separation conditions considering correlations
\begin{figure} \centering \includegraphics[width=0.8\textwidth]{figures/SandBcuts.jpeg} \end{figure}
Multi-variate analyses (MVA)
- Regression - in the multidimensional observable space $(V_1,V_2,....,V_n)$ a functional connection with optimal parameters is determined
\begin{figure} \centering \includegraphics[width=0.8\textwidth]{figures/regression.jpeg} \end{figure}
-
supervised regression: model is known
-
unsupervised regression: model is unknown
-
for the parameter determination Maximum likelihood fits are used
MVA Classification in N Dimensions
For each event there are N measured variables
\begin{figure} \centering \includegraphics[width=0.9\textwidth]{figures/classificationVar.jpeg} \end{figure}
:::: columns :::: {.column width=70%}
-
Search for a mathematical transformation F of the N dimensional input space to a one dimensional output space
F(\vec V) : \mathbb{R}^N \rightarrow \mathbb{R} -
A simple cut in F implements a complex cut in the N dimensional variable space
-
Determine
F(\vec V)using a model and fit the parameters
:::: ::::{.column width=30%} \includegraphics[]{figures/response.jpeg} :::: :::
MVA Classification in N Dimensions
:::: columns :::: {.column width=60%}
- Parameters \newline
Important measures to quantify quality \newline \newline
Efficiency:
\epsilon = \frac{N_S (F>F_0)}{N_s}\newline Purity: $\pi = \frac{N_S (F>F_0)}{(N_s + N_B)(F>F_0)}$ :::: ::::{.column width=40%} \includegraphics[]{figures/response.jpeg} :::: ::: \vspace{0.3cm} :::: columns :::: {.column width=60%} - Reciever Operations Characteristics (ROC) \newline Errors in classification \newline \includegraphics[width=0.7\textwidth]{figures/error.jpeg} :::: ::::{.column width=40%} \includegraphics[]{figures/roc.jpeg} :::: :::
MVA Classification in N Dimensions
:::: columns :::: {.column width=60%}
-
Interpretation of
F(\vec V)-
The distributions of \textcolor{blue}{$F(\vec V|S)$} and \textcolor{red}{$F(\vec V|S)$} are interpreted as probability density functions (PDF), \textcolor{blue}{$PDF_S(F)$} and \textcolor{blue}{$PDF_B(F)$}
-
For a given
F_0the probability for signal and background for a givenS/Bcan be determined \newlineP ( data = S | F)= \frac {\color {blue} {f_S \cdot PDF_S(F)}} { \color {red} {f_B \cdot PDF_B(F)} + \color {blue} {f_S \cdot PDF_S(F)} }:::: ::::{.column width=40%} \includegraphics[]{figures/response.jpeg} :::: ::: \vspace{0.3cm}
-
-
A cut in the one dimensional Variable
F(\vec V) =F_0and accepting all events on the right determines the signal and background efficiency (background rejection). A systematic change ofF(\vec V)gives the ROC curve. \newline
\definecolor{darkgreen}{RGB}{0,125,0}
- \color{darkgreen}{A cut in
F(\vec V)corresponds to a complex hyperplane, which can not neccessarily be described by a function.}
Simple Cuts in Variables
-
The most simple classificator to select signal events are cuts in all variables which show a separation
-
The output is binary and not a probability on
SorB. -
An optimization of the cuts is done by maximizing of the background suppression for given signal efficiencies.
-
Significance
sig = \epsilon_S \cdot N_S / \sqrt{ \epsilon_S \cdot N_S + \epsilon_B( \epsilon_S) N_B}
-
\begin{figure} \centering \includegraphics[width=0.8\textwidth]{figures/cutInVariables.jpeg} \end{figure}
Fisher Discriminat
Idea: Find a plane, that the projection of the data on the plane gives an optimal separation of signal and background
:::: columns :::: {.column width=60%}
-
The Fisher discriminat is the linear combination of all input variables \newline
F(\vec{V}) = \sum_i w_i \cdot V_i = \vec{w}^T \vec{V}\newline -
\vec wdefines the orientation of the plane. The coefficients are defined such that the difference of the expectation values of both classes is large and the variance is small. \newlineJ( \vec{w} ) = \frac {( F_S - F_B )^2}{ \sigma_S^2 + \sigma_B^2 } = \frac { \vec{w}^T K \vec{w} }{ \vec{w}^T L \vec{w} }\newline withKas covariance of the the expectation valuesF_S -F_Band L is the sum -
For the separation a value
F_cis determined. :::: ::::{.column width=40%} \includegraphics[]{figures/fisher.jpeg} :::: :::
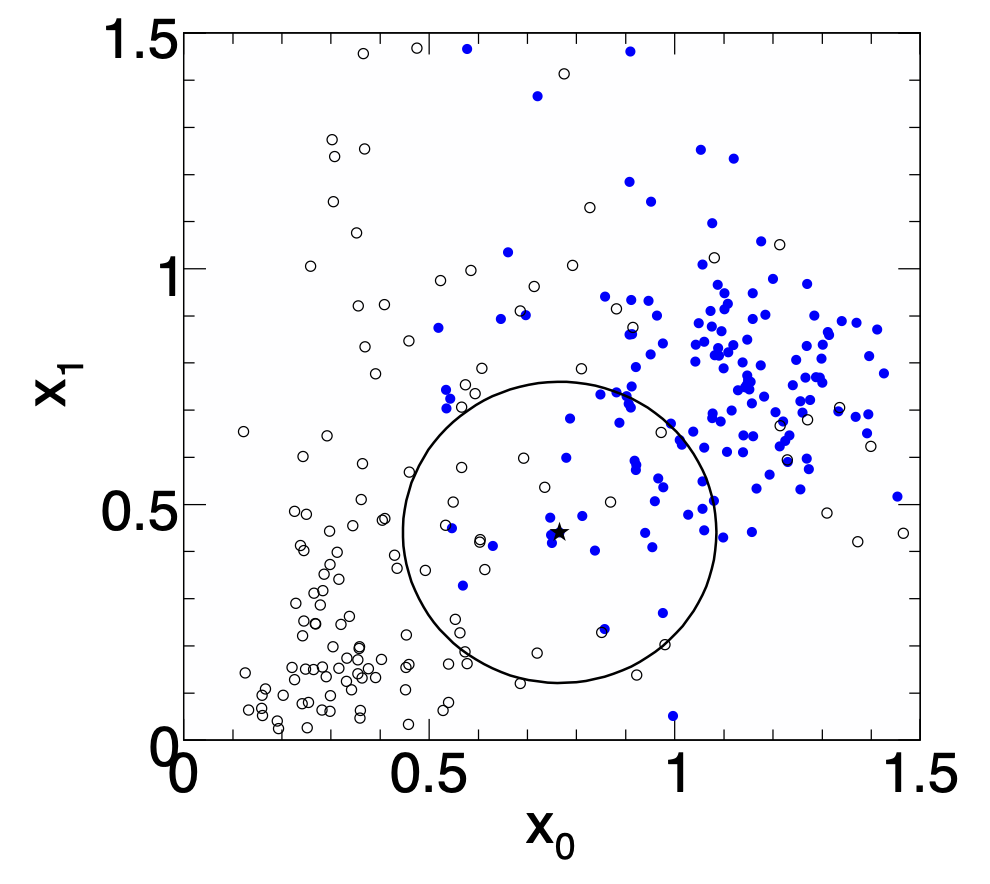
k-Nearest Neighbor Method (1)
$k$-NN classifier:
- Estimates probability density around the input vector
p(\vec x|S)andp(\vec x|B)are approximated by the number of signal and background events in the training sample that lie in a small volume around the point\vec x
\vspace{2ex}
Algorithms finds k nearest neighbors:
k = k_s + k_b Probability for the event to be of signal type:
p_s(\vec x) = \frac{k_s(\vec x)}{k_s(\vec x) + k_b(\vec x)} k-Nearest Neighbor Method (2)
::: columns :::: {.column width=60%} Simplest choice for distance measure in feature space is the Euclidean distance:
R = |\vec x - \vec y|Better: take correlations between variables into account:
R = \sqrt{(\vec{x}-\vec{y})^T V^{-1} (\vec{x}-\vec{y})} V = \text{covariance matrix}, R = \text{"Mahalanobis distance"}::::
:::: {.column width=40%}
 ::::
:::
::::
:::
\vfill
The $k$-NN classifier has best performance when the boundary that separates signal and background events has irregular features that cannot be easily approximated by parametric learning methods.
-
Determination of the underlying data structure (regression problem)
-
MVA Methods
- More effective than classic cut-based analyses
- Take correlations of input variables into account \vfill
-
Important: find good input variables for MVA methods
- Good separation power between S and B
- No strong correlation among variables
- No correlation with the parameters you try to measure in your signal sample! \vfill
-
Pre-processing
- Apply obvious variable transformations and let MVA method do the rest
- Make use of obvious symmetries: if e.g. a particle production process is symmetric in polar angle
\thetause|\cos \theta|and not\cos \thetaas input variable - It is generally useful to bring all input variables to a similar numerical range
Fischer Discriminant
Regression
Logistic regression
Decision Trees
XGBoost example with the iris dataset
MVA stands for "Multivariate Analysis," which is a statistical technique used to analyze data that involves multiple variables. In MVA, the relationships between the variables are studied to identify patterns, trends, and dependencies.
MVA techniques are used in many fields, including finance, engineering, physics, biology, and social sciences. Some common MVA techniques include principal component analysis (PCA), factor analysis, cluster analysis, discriminant analysis, and regression analysis.
PCA, for example, is a commonly used MVA technique that reduces the dimensionality of a data set by identifying the most important variables or components. This can help to simplify data visualization and analysis. Factor analysis, on the other hand, is used to identify underlying factors that contribute to the variation in a set of variables.
Overall, MVA is a powerful tool for analyzing complex data sets and can provide insights into relationships and dependencies that might not be apparent when analyzing individual variables in isolation.
Regenerate response