22 KiB
% Introduction to Data Analysis and Machine Learning in Physics: \ 3. Machine Learning Basics, Multivariate Analysis % Jörg Marks, Klaus Reygers % Studierendentage, 11-14 April 2023
Multi-variate analyses (MVA)
-
General Question \vspace{0.1cm}
There are 2 categories of distinguishable data, S and B, described by discrete variables. What are criteria for a separation of both samples?
- Single criteria are not sufficient to distinguish S and B
- Reduction of the variable space to probabilities for S or B \vspace{0.1cm}
-
Classification of measurements using a set of observables
(V_1,V_2,....,V_n)- find optimal separation conditions considering correlations
\begin{figure} \centering \includegraphics[width=0.8\textwidth]{figures/SandBcuts.jpeg} \end{figure}
Multi-variate analyses (MVA)
- Regression - in the multidimensional observable space $(V_1,V_2,....,V_n)$ a functional connection with optimal parameters is determined
\begin{figure} \centering \includegraphics[width=0.8\textwidth]{figures/regression.jpeg} \end{figure}
-
supervised regression: model is known
-
unsupervised regression: model is unknown
-
for the parameter determination Maximum likelihood fits are used
MVA Classification in N Dimensions
For each event there are N measured variables
\begin{figure} \centering \includegraphics[width=0.9\textwidth]{figures/classificationVar.jpeg} \end{figure}
:::: columns :::: {.column width=70%}
-
Search for a mathematical transformation F of the N dimensional input space to a one dimensional output space
F(\vec V) : \mathbb{R}^N \rightarrow \mathbb{R} -
A simple cut in F implements a complex cut in the N dimensional variable space
-
Determine
F(\vec V)using a model and fit the parameters
:::: ::::{.column width=30%} \includegraphics[]{figures/response.jpeg} :::: :::
MVA Classification in N Dimensions
:::: columns :::: {.column width=60%}
- Parameters \newline
Important measures to quantify quality \newline \newline
Efficiency:
\epsilon = \frac{N_S (F>F_0)}{N_s}\newline Purity: $\pi = \frac{N_S (F>F_0)}{(N_s + N_B)(F>F_0)}$ :::: ::::{.column width=40%} \includegraphics[]{figures/response.jpeg} :::: ::: \vspace{0.3cm} :::: columns :::: {.column width=60%} - Reciever Operations Characteristics (ROC) \newline Errors in classification \newline \includegraphics[width=0.7\textwidth]{figures/error.jpeg} :::: ::::{.column width=40%} \includegraphics[]{figures/roc.jpeg} :::: :::
MVA Classification in N Dimensions
:::: columns :::: {.column width=60%}
-
Interpretation of
F(\vec V)-
The distributions of \textcolor{blue}{$F(\vec V|S)$} and \textcolor{red}{$F(\vec V|S)$} are interpreted as probability density functions (PDF), \textcolor{blue}{$PDF_S(F)$} and \textcolor{blue}{$PDF_B(F)$}
-
For a given
F_0the probability for signal and background for a givenS/Bcan be determined \newlineP ( data = S | F)= \frac {\color {blue} {f_S \cdot PDF_S(F)}} { \color {red} {f_B \cdot PDF_B(F)} + \color {blue} {f_S \cdot PDF_S(F)} }:::: ::::{.column width=40%} \includegraphics[]{figures/response.jpeg} :::: ::: \vspace{0.3cm}
-
-
A cut in the one dimensional Variable
F(\vec V) =F_0and accepting all events on the right determines the signal and background efficiency (background rejection). A systematic change ofF(\vec V)gives the ROC curve. \newline
\definecolor{darkgreen}{RGB}{0,125,0}
- \color{darkgreen}{A cut in
F(\vec V)corresponds to a complex hyperplane, which can not neccessarily be described by a function.}
Simple Cuts in Variables
-
The most simple classificator to select signal events are cuts in all variables which show a separation
-
The output is binary and not a probability on
SorB. -
An optimization of the cuts is done by maximizing of the background suppression for given signal efficiencies.
-
Significance
sig = \epsilon_S \cdot N_S / \sqrt{ \epsilon_S \cdot N_S + \epsilon_B( \epsilon_S) N_B}
-
\begin{figure} \centering \includegraphics[width=0.8\textwidth]{figures/cutInVariables.jpeg} \end{figure}
Fisher Discriminat
Idea: Find a plane, that the projection of the data on the plane gives an optimal separation of signal and background
:::: columns :::: {.column width=60%}
-
The Fisher discriminat is the linear combination of all input variables \newline
F(\vec{V}) = \sum_i w_i \cdot V_i = \vec{w}^T \vec{V}\newline -
\vec wdefines the orientation of the plane. The coefficients are defined such that the difference of the expectation values of both classes is large and the variance is small. \newlineJ( \vec{w} ) = \frac {( F_S - F_B )^2}{ \sigma_S^2 + \sigma_B^2 } = \frac { \vec{w}^T K \vec{w} }{ \vec{w}^T L \vec{w} }\newline withKas covariance of the the expectation valuesF_S -F_Band L is the sum -
For the separation a value
F_cis determined. :::: ::::{.column width=40%} \includegraphics[]{figures/fisher.jpeg} :::: :::
k-Nearest Neighbor Method (1)
$k$-NN classifier:
- Estimates probability density around the input vector
p(\vec x|S)andp(\vec x|B)are approximated by the number of signal and background events in the training sample that lie in a small volume around the point\vec x
\vspace{2ex}
Algorithms finds k nearest neighbors:
k = k_s + k_b Probability for the event to be of signal type:
p_s(\vec x) = \frac{k_s(\vec x)}{k_s(\vec x) + k_b(\vec x)} k-Nearest Neighbor Method (2)
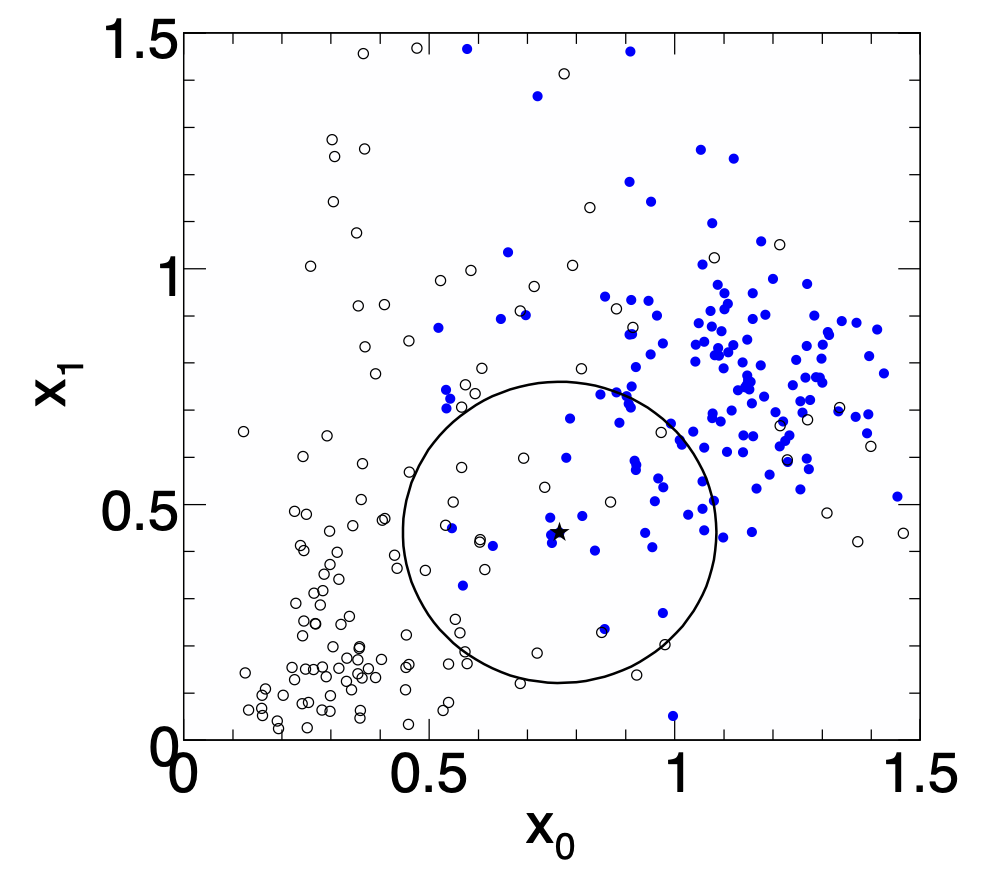
::: columns :::: {.column width=60%} Simplest choice for distance measure in feature space is the Euclidean distance:
R = |\vec x - \vec y|Better: take correlations between variables into account:
R = \sqrt{(\vec{x}-\vec{y})^T V^{-1} (\vec{x}-\vec{y})} V = \text{covariance matrix}, R = \text{"Mahalanobis distance"}::::
:::: {.column width=40%}
 ::::
:::
::::
:::
\vfill
The $k$-NN classifier has best performance when the boundary that separates signal and background events has irregular features that cannot be easily approximated by parametric learning methods.
Linear regression revisited
\vfill
::: columns
:::: {.column width=50%}
\small \textcolor{gray}{"Galton family heights data": \ origin of the term "regression"} \normalsize
:::: :::: {.column width=50%}
- data:
\{x_i,y_i\}\ - objective: predict
y = f(x) - model:
f(x; \vec \theta) = m x + b, \quad \vec \theta = (m, b) - loss function:
J(\theta|x,y) = \frac{1}{N} \sum_{i=1}^N (y_i - f(x_i))^2 - model training: optimal parameters
\hat{\vec{\theta}} = \mathrm{arg\,min} \, J(\vec \theta)
:::: :::
Linear regression
-
Data: vectors with
pcomponents ("features"):\vec x = (x_1, ..., x_p) -
nobservations:\{\vec x_i, y_i\}, \quad i = 1, ..., n -
Prediction for given vector
x:y = w_0 + w_1 x_1 + w_2 x_2 + ... + w_p x_p \equiv \vec w^\intercal \vec x \quad \text{where } x_0 := 1 -
Find weights that minimze loss function:
\hat{\vec{w}} = \underset{\vec w}{\min} \sum_{i=1}^{n} (\vec w^\intercal \vec x_i - y_i)^2 -
In case of linear regression closed-form solution exists:
\hat{\vec{w}} = (X^\intercal X)^{-1} X^\intercal \vec y \quad \text{where} \; X \in \mathbb{R}^{n \times p} -
Xis called the design matrix, rowiofXis\vec x_i
Linear regression with regularization
::: columns :::: {.column width=45%}
-
Standard loss function
C(\vec w) = \sum_{i=1}^{n} (\vec w^\intercal \vec x_i - y_i)^2 -
Ridge regression
C(\vec w) = \sum_{i=1}^{n} (\vec w^\intercal \vec x_i - y_i)^2 + \lambda |\vec w|^2 -
LASSO regression
C(\vec w) = \sum_{i=1}^{n} (\vec w^\intercal \vec x_i - y_i)^2 + \lambda |\vec w|
:::: :::: {.column width=55%}
\vfill

w_j = 0). This is why LASSO regression is also called sparse regression.} \normalsize
::::
:::
Logistic regression (1)
- Consider binary classification task, e.g.,
y_i \in \{0,1\} - Objective: Predict probability for outcome
y=1given an observation\vec x - Starting with linear "score"
s = w_0 + w_1 x_1 + w_2 x_2 + ... + w_p x_p \equiv \vec w^\intercal \vec x - Define function that translates
sinto a quantity that has the properties of a probability\sigma(s) = \frac{1}{1+e^{-s}} - We would like to determine the optimal weights for a given training data set. They result from the maximum-likelihood principle.
Logistic regression (2)
- Consider feature vector
\vec x. For a given set of weights\vec wthe model predicts- a probability
p(1|\vec w) = \sigma(\vec w^\intercal \vec x)for outcomey=1 - a probabiltiy
p(0|\vec w) = 1 - \sigma(\vec w^\intercal \vec x)for outcomey=0
- a probability
- The probability
p(y_i | \vec w)defines the likelihoodL_i(\vec w) = p(y_i | \vec w)(the likelihood is a function of the parameters\vec wand the observationsy_iare fixed). - Likelihood for the full data sample (
nobservations)L(\vec w) = \prod_{i=1}^n L_i(\vec w) = \prod_{i=1}^n \sigma(\vec w^\intercal \vec x)^{y_i} \,(1-\sigma(\vec w^\intercal \vec x))^{1-y_i} - Maximizing the log-likelihood
\ln L(\vec w)corresponds to minimizing the loss functionC(\vec w) = - \ln L(\vec w) = \sum_{i=1}^n - y_i \ln \sigma(\vec w^\intercal \vec x) -
(1-y_i) \ln(1-\sigma(\vec w^\intercal \vec x))
- This is nothing else but the cross-entropy loss function
Example 1 - Probability of passing an exam (logistic regression) (1)
Objective: predict the probability that someone passes an exam based on the number of hours studying
p_\mathrm{pass} = \sigma(s) = \frac{1}{1+e^{-s}}, \quad s = w_1 t + w_0, \quad t = \text{\# hours}::: columns :::: {.column width=40%}
- Data set: \
- preparation
ttime in hours - passed / not passes (0/1)
- preparation
- Parameters need to be determined through numerical minimization
w_0 = -4.0777w_1 = 1.5046
\vspace{1.5ex}
\footnotesize
\textcolor{gray}{03_ml_basics_logistic_regression.ipynb}
\normalsize
::::
:::: {.column width=60%}

Example 1 - Probability of passing an exam (logistic regression) (2)
\footnotesize \textcolor{gray}{Read data from file:}
# data: 1. hours studies, 2. passed (0/1)
df = pd.read_csv(filename, engine='python', sep='\s+')
x_tmp = df['hours_studied'].values
x = np.reshape(x_tmp, (-1, 1))
y = df['passed'].values
\vfill \textcolor{gray}{Fit the data:}
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(penalty='none', fit_intercept=True)
clf.fit(x, y);
\vfill \textcolor{gray}{Calculate predictions:}
hours_studied_tmp = np.linspace(0., 6., 1000)
hours_studied = np.reshape(hours_studied_tmp, (-1, 1))
y_pred = clf.predict_proba(hours_studied)
\normalsize
Precision and recall
::: columns
:::: {.column width=50%}
\textcolor{blue}{Precision:}
Fraction of correctly classified instances among all instances that obtain a certain class label.
\text{precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} \begin{center} \textcolor{gray}{"purity"} \end{center}
::::
:::: {.column width=50%}
\textcolor{blue}{Recall:}
Fraction of positive instances that are correctly classified.
\vspace{2.9ex}
\text{recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} \begin{center} \textcolor{gray}{"efficiency"} \end{center}
:::: ::: \vfill \begin{center} \textcolor{gray}{TP: true positives, FP: false positives, FN: false negatives} \end{center}
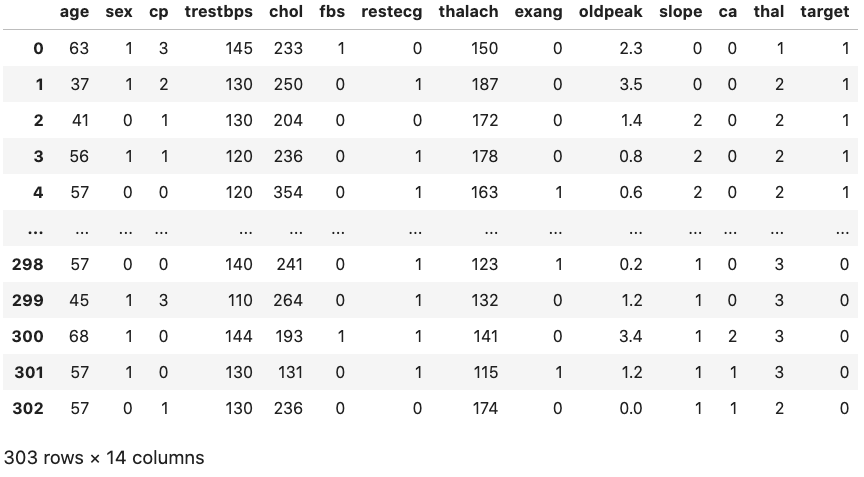
Example 2: Heart disease data set (logistic regression) (1)
\scriptsize \textcolor{gray}{Read data:}
filename = "https://www.physi.uni-heidelberg.de/~reygers/lectures/2023/ml/data/heart.csv"
df = pd.read_csv(filename)
df
\vfill
 {width=70%}
\normalsize
\vspace{1.5ex}
\footnotesize
\textcolor{gray}{03_ml_basics_log_regr_heart_disease.ipynb}
\normalsize
{width=70%}
\normalsize
\vspace{1.5ex}
\footnotesize
\textcolor{gray}{03_ml_basics_log_regr_heart_disease.ipynb}
\normalsize
Example 2: Heart disease data set (logistic regression) (2)
\footnotesize
\textcolor{gray}{Define array of labels and feature vectors}
y = df['target'].values
X = df[[col for col in df.columns if col!="target"]]
\vfill \textcolor{gray}{Generate training and test data sets}
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, shuffle=True)
\vfill \textcolor{gray}{Fit the model}
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(penalty='none', fit_intercept=True, max_iter=1000, tol=1E-5)
lr.fit(X_train, y_train)
\normalsize
Example 2: Heart disease data set (logistic regression) (3)
\footnotesize \textcolor{gray}{Test predictions on test data set:}
from sklearn.metrics import classification_report
y_pred_lr = lr.predict(X_test)
print(classification_report(y_test, y_pred_lr))
\vfill \textcolor{gray}{Output:}
precision recall f1-score support
0 0.75 0.86 0.80 63
1 0.89 0.80 0.84 89
accuracy 0.82 152
macro avg 0.82 0.83 0.82 152
weighted avg 0.83 0.82 0.82 152
Example 2: Heart disease data set (logistic regression) (4)
\textcolor{gray}{Compare to another classifier usinf the \textit{receiver operating characteristic} (ROC) curve} \vfill \textcolor{gray}{Let's take the random forest classifier} \footnotesize
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(max_depth=3)
rf.fit(X_train, y_train)
\normalsize \vfill \textcolor{gray}{Use \texttt{roc_curve} from scikit-learn} \footnotesize
from sklearn.metrics import roc_curve
y_pred_prob_lr = lr.predict_proba(X_test) # predicted probabilities
fpr_lr, tpr_lr, _ = roc_curve(y_test, y_pred_prob_lr[:,1])
y_pred_prob_rf = rf.predict_proba(X_test) # predicted probabilities
fpr_rf, tpr_rf, _ = roc_curve(y_test, y_pred_prob_rf[:,1])
\normalsize
Example 2: Heart disease data set (logistic regression) (5)
::: columns :::: {.column width=50%} \scriptsize
plt.plot(tpr_lr, 1-fpr_lr, label="log. regression")
plt.plot(tpr_rf, 1-fpr_rf, label="random forest")
\vspace{5ex}
\normalsize \textcolor{gray}{Classifiers can be compared with the \textit{area under curve} (AUC) score.} \scriptsize
from sklearn.metrics import roc_auc_score
auc_lr = roc_auc_score(y_test,y_pred_lr)
auc_rf = roc_auc_score(y_test,y_pred_rf)
print(f"AUC scores: {auc_lr:.2f}, {auc_knn:.2f}")
\vspace{5ex} \normalsize \textcolor{gray}{This gives} \scriptsize
AUC scores: 0.82, 0.83
\normalsize
:::: :::: {.column width=50%} \begin{figure} \centering \includegraphics[width=0.96\textwidth]{figures/03_ml_basics_log_regr_heart_disease.pdf} \end{figure} :::: :::
Multinomial logistic regression: Softmax function
In the previous example we considered two classes (0, 1). For multi-class classification, the logistic function can generalized to the softmax function.
\vfill
Now consider k classes and let s_i be the score for class i: $\vec s = (s_1, ..., s_k)$
\vfill
A probability for class i can be predicted with the softmax function:
\sigma(\vec s)i = \frac{e^{s_i}}{\sum{j=1}^k e^{s_j}} \quad \text{ for } \quad i = 1, ... , k $$
The softmax functions is often used as the last activation function of a neural network in order to predict probabilities in a classification task.
\vfill
Multinomial logistic regression is also known as softmax regression.
Example 3: Iris data set (softmax regression) (1)
Iris flower data set
- Introduced 1936 in a paper by Ronald Fisher
- Task: classify flowers
- Three species: iris setosa, iris virginica and iris versicolor
- Four features: petal width and length, sepal width/length, in centimeters
::: columns :::: {.column width=40%} \begin{figure} \centering \includegraphics[width=0.95\textwidth]{figures/iris_dataset.png} \end{figure} :::: :::: {.column width=60%}
\vspace{2ex}
\footnotesize \textcolor{gray}{03_ml_basics_iris_softmax_regression.ipynb}
\vspace{19ex}
\scriptsize https://archive.ics.uci.edu/ml/datasets/Iris
https://en.wikipedia.org/wiki/Iris_flower_data_set \normalsize :::: :::
Example 3: Iris data set (softmax regression) (2)
\textcolor{gray}{Get data set} \footnotesize
# import some data to play with
# columns: Sepal Length, Sepal Width, Petal Length and Petal Width
iris = datasets.load_iris()
X = iris.data
y = iris.target
# split data into training and test data sets
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=42)
\normalsize \vfill
\textcolor{gray}{Softmax regression} \footnotesize
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(multi_class='multinomial', penalty='none')
log_reg.fit(x_train, y_train);
\normalsize
Example 3 : Iris data set (softmax regression) (3)
::: columns :::: {.column width=70%} \textcolor{gray}{Accuracy and confusion matrix for different classifiers} \footnotesize
for clf in [log_reg, kn_neigh, fisher_ld]:
y_pred = clf.predict(x_test)
acc = accuracy_score(y_test, y_pred)
print(type(clf).__name__)
print(f"accuracy: {acc:0.2f}")
# confusion matrix:
# columns: true class, row: predicted class
print(confusion_matrix(y_test, y_pred),"\n")
\normalsize :::: :::: {.column width=30%}
\footnotesize
LogisticRegression
accuracy: 0.96
[[29 0 0]
[ 0 23 0]
[ 0 3 20]]
KNeighborsClassifier
accuracy: 0.95
[[29 0 0]
[ 0 23 0]
[ 0 4 19]]
LinearDiscriminantAnalysis
accuracy: 0.99
[[29 0 0]
[ 0 23 0]
[ 0 1 22]]
\normalsize :::: :::
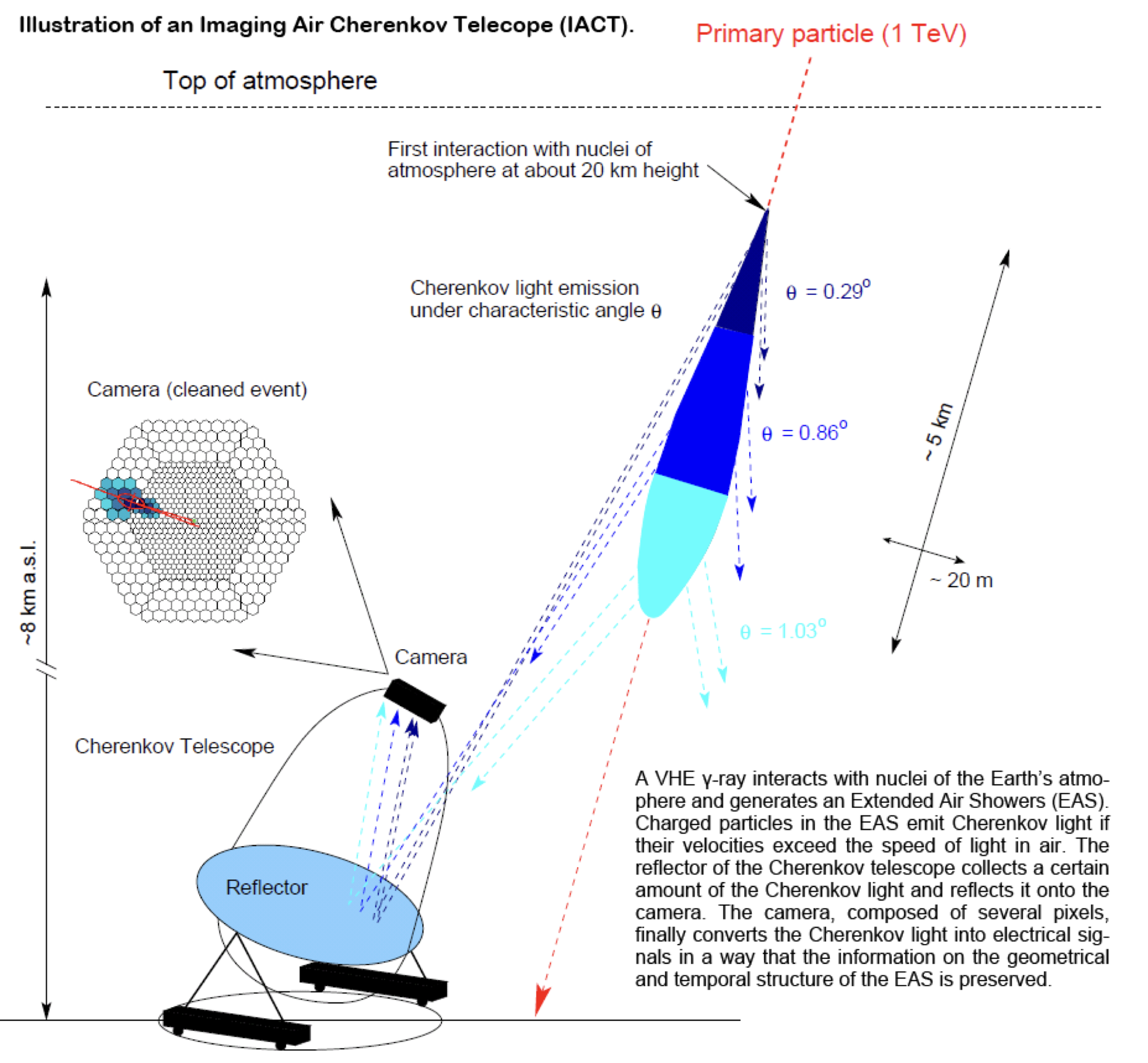
Exercise 1: Classification of air showers measured with the MAGIC telescope
::: columns :::: {.column width=50%}
\small
- Cosmic gamma rays (30 GeV - 30 TeV).
- Cherenkov light from air showers
- Background: air showers caused by hadrons. \normalsize
\begin{figure}
\centering
\includegraphics[width=0.85\textwidth]{figures/magic_photo_small.png}
\end{figure}
::::
:::: {.column width=50%}
 ::::
:::
::::
:::
Exercise 1: Classification of air showers measured with the MAGIC telescope
\begin{figure} \centering \includegraphics[width=0.75\textwidth]{figures/magic_shower_em_had_small.png} \end{figure} ::: columns :::: {.column width=50%} \begin{center} Gamma shower \end{center} :::: :::: {.column width=50%} \begin{center} Hadronic shower \end{center} :::: :::
Exercise 1: Classification of air showers measured with the MAGIC telescope
\begin{figure} \centering \includegraphics[width=0.95\textwidth]{figures/magic_shower_parameters.png} \end{figure}
Exercise 1: Classification of air showers measured with the MAGIC telescope
MAGIC data set
\tiny
\textcolor{gray}{https://archive.ics.uci.edu/ml/datasets/magic+gamma+telescope}
\normalsize
\scriptsize
1. fLength: continuous # major axis of ellipse [mm]
2. fWidth: continuous # minor axis of ellipse [mm]
3. fSize: continuous # 10-log of sum of content of all pixels [in #phot]
4. fConc: continuous # ratio of sum of two highest pixels over fSize [ratio]
5. fConc1: continuous # ratio of highest pixel over fSize [ratio]
6. fAsym: continuous # distance from highest pixel to center, projected onto major axis [mm]
7. fM3Long: continuous # 3rd root of third moment along major axis [mm]
8. fM3Trans: continuous # 3rd root of third moment along minor axis [mm]
9. fAlpha: continuous # angle of major axis with vector to origin [deg]
10. fDist: continuous # distance from origin to center of ellipse [mm]
11. class: g,h # gamma (signal), hadron (background)
g = gamma (signal): 12332
h = hadron (background): 6688
For technical reasons, the number of h events is underestimated.
In the real data, the h class represents the majority of the events.
\normalsize
Exercise 1: Classification of air showers measured with the MAGIC telescope
\small \textcolor{gray}{03_ml_basics_ex_1_magic.ipynb} \normalsize
a) Create for each variable a figure with a plot for gammas and hadrons overlayed. b) Create training and test data set. The test data should amount to 50% of the total data set. c) Define the logistic regressor and fit the training data d) Determine the model accuracy and the AUC score e) Plot the ROC curve (background rejection vs signal efficiency)
General remarks on multi-variate analyses (MVAs)
- MVA Methods
- More effective than classic cut-based analyses
- Take correlations of input variables into account \vfill
- Important: find good input variables for MVA methods
- Good separation power between S and B
- No strong correlation among variables
- No correlation with the parameters you try to measure in your signal sample! \vfill
- Pre-processing
- Apply obvious variable transformations and let MVA method do the rest
- Make use of obvious symmetries: if e.g. a particle production process is symmetric in polar angle
\thetause|\cos \theta|and not\cos \thetaas input variable - It is generally useful to bring all input variables to a similar numerical range
Example of feature transformation
\begin{figure} \centering \includegraphics[width=0.95\textwidth]{figures/feature_transformation.png} \end{figure}
Exercise 2: Data preprocessing
a) Read the description of the sklearn.preprocessing package.
b) Start from the example notebook on the logistic regression for the heart disease data set (03_ml_basics_log_regr_heart_disease.ipynb). Pre-process the heart disease data set according to the given example. Does preprocessing make a difference in this case?
